Propagation dans une couche convolutive

Propagation dans une couche convolutive

Objectif

On cherche à calculer comment se fait la propagation de l’information dans une couche convolutive: Les notations de ce post reprennent celles proposées dans le cours de Stanford CS231n: Convolutional Neural Networks for Visual Recognition. Cet article présente les étapes de la construction d’un algorithme simple pour la propagation dans une couche convolutive.

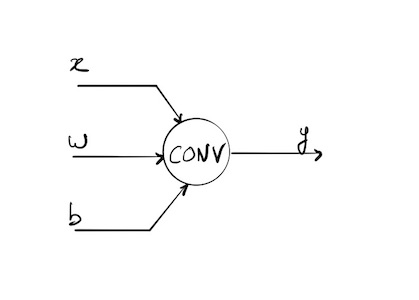
Paramètres en entrée et sortie de la couche convolutive

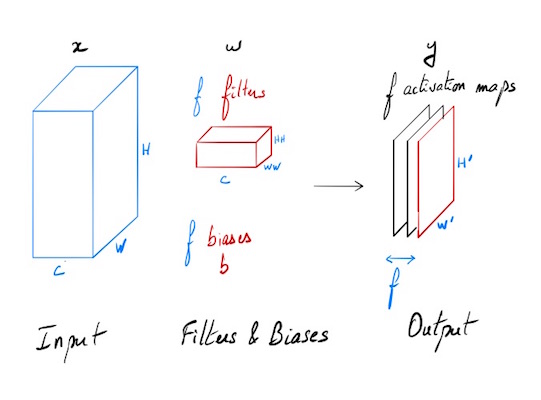
On dispose d’une entrée x de N points, chacun avec C canaux, une hauteur de H, et une largeur de W. On effectue un produit de convolution avec F filtres différents w, sur l’intégralité de la profondeur C, chaque filtre a pour hauteur HH et comme largeur WW.

Entrées:

• x: données d’entrée de dimensions (N, C, H, W)
• w: poids de filtres de dimensions (F, C, HH, WW)
• b: Biais de dimensions (F,)
• conv_param: un dictionnaire de paramètres avec les entrées suivantes:
  • ‘stride’: Le nombre de pixel entre deux zones successives d’application du filtre (identiques en largeur et en hauteur).
  • ‘pad’: Le nombre de pixel pour effectuer un remplissage à 0 (“0-padding”) autour de l’entrée. Ce remplissage est fait de manière symétrique selon les différents axes.

Sortie:

• out: Données de sortie de dimension (N, F, H’, W’) où H’ and W’ sont définis par:
  • H’ = 1 + (H + 2 * pad - HH) / stride
  • W’ = 1 + (W + 2 * pad - WW) / stride
• cache: données mémorisées pour la rétropropagation (x, w, b, conv_param)

Produit de convolution

Cas général simplifié où N=1, C=1, F=1, stride=1, pad=0

N=1 une seule entrée, C=1 un seul canal, F=1 un seul filtre.

Pas de biais

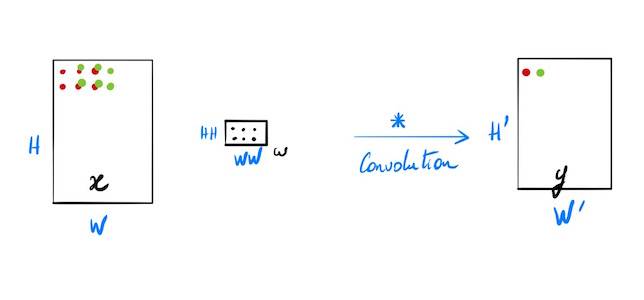
• x: données d’entrée de dimensions (H, W)
• w: poids de filtres de dimensions (HH, WW)
• y: sortie de dimensions (H’, W’)
  • H’ = 1 + (H - HH)
  • W’ = 1 + (W - WW)

\[\forall (i,j) \in [1,H'] \times [1,W']\] \[y_{ij} = \sum_{k} \sum_{l} w_{kl} \cdot x_{i+k-1,j+l-1} \tag {1}\]

Cas particulier simple

Détail de la construction du produit de convolution simplifié avant généralisation

x = np.array([[[1, 2], [7, 4]],[[2, 3], [8, 3]],[[1, 1], [1, 1]]])

xp = x avec 0-padding de 1 sur chacun des canaux

xp = np.pad(x,((0,), (1,), (1, )), 'constant')

array([[[0, 0, 0, 0],
        [0, 1, 2, 0],
        [0, 7, 4, 0],
        [0, 0, 0, 0]],

       [[0, 0, 0, 0],
        [0, 2, 3, 0],
        [0, 8, 3, 0],
        [0, 0, 0, 0]],

       [[0, 0, 0, 0],
        [0, 1, 1, 0],
        [0, 1, 1, 0],
        [0, 0, 0, 0]]])

Définition d’un filtre w de taille 2x2 ( et toute la profondeur du volume d’entrée)

w = np.array([[[0, 0],[0, 1]], [[0, 0],[0, 2]], [[0, 0],[0, 1]]])
w.shape

(3, 2, 2)

Dimensions de la sortie:

stride = 1
pad = 1
_, HH, WW = w.shape
H_ = int(1 + (H + 2 * pad - HH) / stride) # H'
W_ = int(1 + (W + 2 * pad - WW) / stride) # W'
H_, W_

(3, 3)

Transformation en vecteur pour simplifier l’écriture du produit de convolution sous la forme d’un produit matriciel.

w = w.reshape(-1)
w

array([0, 0, 0, 1, 0, 0, 0, 2, 0, 0, 0, 1])

Extraction du premier élément sur lequel va s’effectuer le produit de convolution:

premier_elt = xp[:, 0:2, 0:2]
premier_elt

array([[[0, 0],
        [0, 1]],

       [[0, 0],
        [0, 2]],

       [[0, 0],
        [0, 1]]])

np.matmul(premier_elt.reshape(-1), w.T)

6

second_elt = xp[:, 1:3, 1:3]
np.matmul(second_elt.reshape(-1), w.T)

11

Effet de la couche convolutive avec un filtre sans biais:

y = np.zeros((H_, W_))
for i in range(H_):
    for j in range(W_):
        input_volume = xp[:, i*stride:i*stride+HH, j*stride:j*stride+WW]
        y[i,j] = np.matmul(input_volume.reshape(-1), w.T)
y

array([[ 6.,  9.,  0.],
       [24., 11.,  0.],
       [ 0.,  0.,  0.]])

Généralisation