Rétropropagation dans une couche convolutive
Rétropropagation dans une couche convolutive - DRAFT eq# à revoir
En travaillant sur le cours de Stanford CS231n: Convolutional Neural Networks for Visual Recognition, je me suis heurté au manque d’information pour coder la rétropropagation dans une couche convolutive. Cet article présente les étapes de la construction de la solution mathématique et la mise en place de l’algorithme pour répondre à ce problème.

Introduction
Motivation
Le but de cet article est de présenter la rétropropagation du gradient dans une couche convolutive. La sortie de cette couche ira dans une fonction d’activation de type relu, et l’on suppose que l’on reçoit le gradient dy rétropropagé depuis cette fonction d’activation. Ayant trouvé peu d’informations détaillées sur le processus et les mathématiques sous-jacentes, cet article détaille pas à pas les étapes de la mise en place d’une solution informatique pour le calcul de ce gradient. On suppose que le lecteur est déjà familier des notions de propagation et rétropropagation dans les réseaux neuronaux, des graphes de calculs et du calcul des gradients de tenseurs.
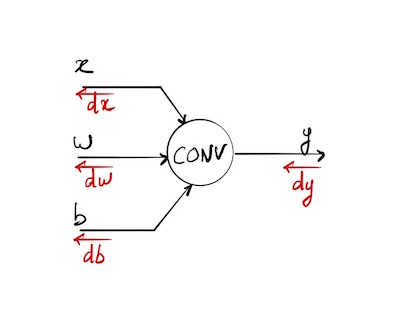
Notations utilisées
On note * le produit de convolution entre deux tenseurs, typiquement une entrée xet un filtre w
- Dans le cas où les tenseurs sont de même taille et avec une ou deux dimensions, cela correspond à la somme de produits de chacun des éléments terme à terme
- Si le filtre
west plus petit quex, on obtient une “carte d’activation”yoù chacun des termes correspond au produit de convolution d’un sous ensemble dexavecw,wse déplaçant sur toute la surface dex. - Si
xetwont plus de deux dimensions on ne considère que les deux dernières dimensions pour effectuer les déplacements du sous ensemble choisi, les produits de convolution se feront sur une dimension supplementaire correspondant à la profondeur.
Les variables et notations utilisées correspondent à l’excellent cours de Stanford et aux exercices de l’assignment 2. Un descriptif du fonctionnement de la propagation dans une couche convolutive est proposé dans cette vidéo et un petit exemple de mise en application dans cet article.
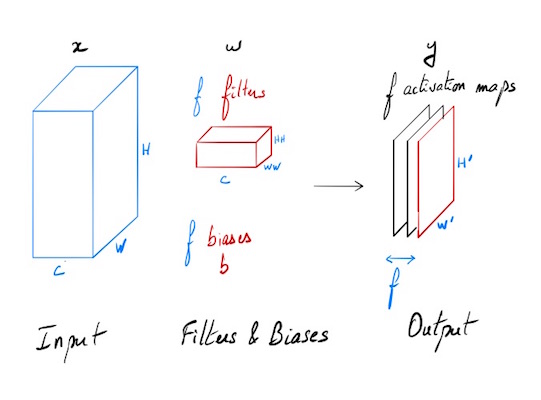
Objectif
On cherche à calculer comment se rétropropage le gradient dans le cas suivant:
On dispose d’une entrée x de N points, chacun avec C canaux, une hauteur de H, et une largeur de W. On effectue un produit de convolution avec F filtres différents w, sur l’intégralité de la profondeur C, chaque filtre a pour hauteur HH et comme largeur WW.
Entrées:
- x: données d’entrée de dimensions (N, C, H, W)
- w: poids de filtres de dimensions (F, C, HH, WW)
- b: Biais de dimensions (F,)
- conv_param: un dictionnaire de paramètres avec les entrées suivantes:
- ‘stride’: Le nombre de pixel entre deux zones successives d’application du filtre (identiques en largeur et en hauteur).
- ‘pad’: Le nombre de pixel pour effectuer un remplissage à 0 (“0-padding”) autour de l’entrée. Ce remplissage est fait de manière symétrique selon les différents axes.
Sortie:
- out: Données de sortie de dimension (N, F, H’, W’) où H’ and W’ sont définis par:
- H’ = 1 + (H + 2 * pad - HH) / stride
- W’ = 1 + (W + 2 * pad - WW) / stride
- cache: données mémorisées pour la rétropropagation (x, w, b, conv_param)
Propagation
Cas général simplifié où N=1, C=1, F=1
N=1 une seule entrée, C=1 un seul canal, F=1 un seul filtre.
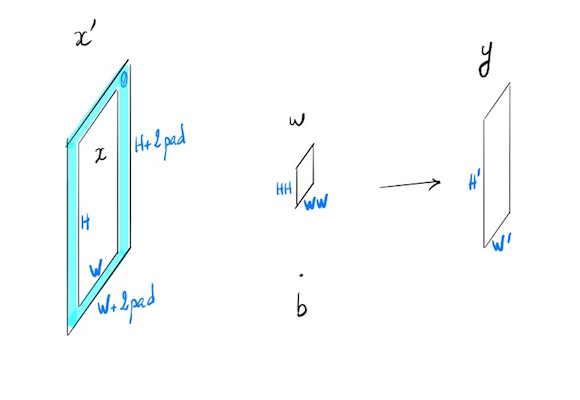
- $x$ : $H \times W$
- $x’ = x$ avec padding
- $w$ : $HH \times WW$
- $b$ biais : scalaire
- $y$ : $H’\times W’$
- stride $s$
$\forall (i,j) \in [1,H’] \times [1,W’]$
\[y_{ij} = \left (\sum_{k=1}^{HH} \sum_{l=1}^{WW} w_{kl} x'_{si+k-1,sj+l-1} \right ) + b \tag {1}\]Cas particulier: stride=1, pad=0, et pas de biais
\[y_{ij} = \sum_{k} \sum_{l} w_{kl} \cdot x_{i+k-1,j+l-1} \tag {1}\]Rétropropagation
On connait
$dy = \left(\frac{\partial L}{\partial y_{ij}}\right)$
On cherche $dx$, $dw$ et $db$, dérivées partielles respectives de notre fonction de coût dont le gradient a été rétropropagé jusqu’à y.
Cas d’un vecteur d’entrée x à 1 dimension
Pour essayer d’avoir une première intuition du résultat et voir comment les choses se mettent en place, on va se limiter dans un premier temps à un exemple très simple.
En entrée
\[x = \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix}\] \[w = \begin{bmatrix} w_1\\ w_2 \end{bmatrix}\] \[b\]En sortie
\[y = \begin{bmatrix} y_1\\ y_2\\ y_3 \end{bmatrix}\]Propagation - convolution avec le filtre w, stride = 1, padding = 0
\[y_1 = w_1 x_1 + w_2 x_2 + b\\ y_2 = w_1 x_2 + w_2 x_3 + b \tag{1}\\ y_3 = w_1 x_3 + w_2 x_4 + b\]Rétropropagation
On connait le gradient de notre fonction de coût L par rapport à y:
\[dy = \frac{\partial L}{\partial y}\]En fait $dy = \frac{\partial L}{\partial y}$, dérivée d’un scalaire par rapport à un vecteur s’écrit avec la notation du Jacobien:
\[\begin{align*} & dy = \begin{bmatrix} \frac{\partial L}{\partial y_1} & \frac{\partial L}{\partial y_2} & \frac{\partial L}{\partial y_3} \end{bmatrix} \\ & dy = \begin{bmatrix} dy_1 & dy_2 & dy_3 \end{bmatrix} \end{align*}\]dy a les mêmes dimensions que y, écriture sous forme vectorielle:
\[dy = (dy_1 , dy_2 , dy_3)\]On cherche
\[dx=\frac{\partial L}{\partial x}, dw=\frac{\partial L}{\partial w}, db=\frac{\partial L}{\partial b}\]db
\[db=\frac{\partial L}{\partial y}\cdot \frac{\partial y}{\partial b} = dy\cdot\frac{\partial y}{\partial b}\]Et la composée de fonction s’écrit sous la forme (en incorporant la formule de propagation (1)):
\[db = \sum_{j}\frac{\partial L}{\partial y_j}\cdot \frac{\partial y_j}{\partial b} = \begin{bmatrix} dy_1 & dy_2 & dy_3 \end{bmatrix} \cdot \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}\] \[\Rightarrow db=dy_1+dy_2+dy_3\]dw
\[dw=\frac{\partial L}{\partial y}\cdot \frac{\partial y}{\partial w} = dy\cdot\frac{\partial y}{\partial w}\] \[\frac{\partial y}{\partial w} = \begin{bmatrix} \frac{\partial y_1}{\partial w_1} & \frac{\partial y_1}{\partial w_2}\\ \frac{\partial y_2}{\partial w_1} & \frac{\partial y_2}{\partial w_2}\\ \frac{\partial y_3}{\partial w_1} & \frac{\partial y_3}{\partial w_2}\\ \end{bmatrix}\] \[\frac{\partial y}{\partial w} = \begin{bmatrix} x_1 & x_2\\ x_2 & x_3\\ x_3 & x_4\\ \end{bmatrix}\] \[\begin{bmatrix} dy_1 & dy_2 & dy_3 \end{bmatrix} \cdot \begin{bmatrix} x_1 & x_2\\ x_2 & x_3\\ x_3 & x_4\\ \end{bmatrix}\] \[dw_1 = x_1 dy_1 + x_2 dy_2 + x_3 dy_3 \\ dw_2 = x_2 dy_1 + x_3 dy_2 + x_4 dy_3\]On peut remarquer que dw correspond au produit de convolution de x avec dy comme filtre, à voir si cela se généralise avec une dimension supplémentaire.
\[dw = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} * \begin{bmatrix} dy_1 \\ dy_2 \\ dy_3 \end{bmatrix}\]dx
\[dx=\frac{\partial L}{\partial y}\cdot \frac{\partial y}{\partial x} = dy^T\cdot\frac{\partial y}{\partial x}\] \[\frac{\partial y}{\partial x} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \frac{\partial y_1}{\partial x_3} & \frac{\partial y_1}{\partial x_4}\\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \frac{\partial y_2}{\partial x_3} & \frac{\partial y_2}{\partial x_4}\\ \frac{\partial y_3}{\partial x_1} & \frac{\partial y_3}{\partial x_2} & \frac{\partial y_3}{\partial x_3} & \frac{\partial y_3}{\partial x_4}\\ \end{bmatrix}\] \[\frac{\partial y}{\partial x} = \begin{bmatrix} w_1 & w_2 & 0 & 0\\ 0 & w_1 & w_2 & 0\\ 0 & 0 & w_1 & w_2\\ \end{bmatrix}\] \[\begin{align*} &dx_1 = w_1 dy_1\\ &dx_2 = w_2 dy_1 + w_1 dy_2 \\ &dx_3 = w_2 dy_2 + w_1 dy_3 \\ &dx_4 = w_2 dy_3 \end{align*}\]Donne encore un produit de convolution, un peu particulier cette fois, il faudrait considérer dy avec un padding à 0 de taille 1, et en faire le produit convolutif avec un filtre w inversé du type $(w_2, w_1)$
\[dx = \begin{bmatrix} 0 \\ dy_1 \\ dy_2 \\ dy_3 \\ 0 \end{bmatrix} * \begin{bmatrix} w_2 \\ w_1 \end{bmatrix}\]On va essayer de généraliser ces résultats en choisissant comme x et w des matrices de petites tailles.
Cas d’une entrée x à 2 dimensions
En entrée
\[x = \begin{bmatrix} x_{11} &x_{12} &x_{13} &x_{14}\\ x_{21} &x_{22} &x_{23} &x_{24} \\ x_{31} &x_{32} &x_{33} &x_{34}\\ x_{41} &x_{42} &x_{43} &x_{44} \end{bmatrix}\] \[w = \begin{bmatrix} w_{11} &w_{12}\\ w_{21} &w_{22} \end{bmatrix}\] \[b\]En sortie
De nouveau on va prendre le cas le plus simple, stride de 1 et pas de padding. Donc $y$ aura pour dimension $3 \times 3$
\[y = \begin{bmatrix} y_{11} &y_{12} &y_{13} \\ y_{21} &y_{22} &y_{23} \\ y_{31} &y_{32} &y_{33} \end{bmatrix}\]Propagation
Ce qui nous donne:
\[y_{11} = w_{11} x_{11} + w_{12} x_{12} + w_{21} x_{21} + w_{22} x_{22} + b\\ y_{12} = w_{11} x_{12} + w_{12} x_{13} + w_{21} x_{22} + w_{22} x_{23} + b\\ \cdots\]En écriture indicielle:
\[y_{ij} = \left (\sum_{k=1}^{2} \sum_{l=1}^{2} w_{kl} x_{i+k-1,j+l-1} \right ) + b \quad \forall(i,j)\in\{1,2,3\}^2 \tag {2}\]Rétropropagation
On connait:
\[dy_{ij} = \frac{\partial L}{\partial y_{ij}}\]db
En utilisant la convention d’Einstein pour alléger les notations (la répétition d’un indice indique la somme sur l’ensemble de la plage de valeurs de cet indice)
\[db = dy_{ij}\cdot\frac{\partial y_{ij}}{\partial b}\]On a une double somme sur i et j, et $\forall (i,j)$ on a $\frac{\partial y_{ij}}{\partial b}=1$, donc
\[db = \sum_{i=1}^3 \sum_{j=1}^3 dy_{ij}\]dw
\[dw=\frac{\partial L}{\partial y_{ij}}\cdot \frac{\partial y_{ij}}{\partial w} = dy\cdot\frac{\partial y}{\partial w}\] \[dw_{mn} = dy_{ij}\cdot\frac{\partial y_{ij}}{\partial w_{mn}} \tag{3}\]On cherche
\[\frac{\partial y_{ij}}{\partial w_{mn}}\]En incorporant l’équation (2) on obtient:
\[\frac{\partial y_{ij}}{\partial w_{mn}} = \sum_{k=1}^{2} \sum_{l=1}^{2} \frac{\partial w_{kl}}{\partial w_{mn}} x_{i+k-1,j+l-1}\]Tous les termes $\frac{\partial w_{kl}}{\partial w_{mn}}$ sont nuls sauf pour $(k,l) = (m,n)$ où cela vaut 1, cas qui n’apparaît qu’une seule fois dans la double somme.
D’où:
\[\frac{\partial y_{ij}}{\partial w_{mn}} = x_{i+k-1,j+l-1}\]En remplaçant dans (3) on obtient:
\[dw_{mn} = dy_{ij} \cdot x_{i+k-1,j+l-1}\] \[\Rightarrow dw_{mn} = \sum_{i=1}^3 \sum_{j=1}^3 dy_{ij} \cdot x_{i+k-1,j+l-1}\]Si l’on compare cette équation avec l’équation 2 qui donne la formule d’un produit de convolution, on retrouve une structure similaire où dy joue le rôle de filtre que l’on applique sur x.
\[dw = \begin{bmatrix} x_{11} &x_{12} &x_{13} &x_{14}\\ x_{21} &x_{22} &x_{23} &x_{24} \\ x_{31} &x_{32} &x_{33} &x_{34}\\ x_{41} &x_{42} &x_{43} &x_{44} \end{bmatrix} * \begin{bmatrix} dy_{11} &dy_{12} &dy_{13} \\ dy_{21} &dy_{22} &dy_{23} \\ dy_{31} &dy_{32} &dy_{33} \end{bmatrix}\] \[dw = x * dy\]dx
En utilisant la loi de composition comme pour (3) on obtient:
\[dx_{mn} = dy_{ij}\cdot\frac{\partial y_{ij}}{\partial x_{mn}} \tag{4}\]Cette fois ci on cherche
\[\frac{\partial y_{ij}}{\partial x_{mn}}\]En incorporant l’équation (2) on obtient:
\[\frac{\partial y_{ij}}{\partial x_{mn}} = \sum_{k=1}^{2} \sum_{l=1}^{2} w_{kl} \frac{\partial x_{i+k-1,j+l-1}}{\partial x_{mn}} \tag{5}\]On a
\[\frac{\partial x_{i+k,j+l}}{\partial x_{mn}} = \begin{cases} 1 & \text{si } m=i+k-1 \text{ et } n=j+l-1\\ 0 & \text{sinon } \end{cases}\] \[\begin{cases} m=i+k-1\\ n=j+l-1 \end{cases}\] \[\Rightarrow \begin{cases} k=m-i+1\\ l=n-j+1 \end{cases} \tag{6}\]Dans notre exemple on a
\[\begin{align*} &m,n \in [1,4] & \text{ entrées }\\ &k,l \in [1,2] & \text{ filtres }\\ &i,j \in [1,3] & \text{ sorties } \end{align*}\]Donc lorsque l’on fait $k=m-i+1$, on va sortir un peu de l’intervalle de valeurs, $(m-i+1) \in [-1,4]$, donc pour garder la cohérence dans la formule (5) on va étendre la matrice $w$ avec des $0$ dès que les valeurs des indices sortiront de l’intervalle de définition.
De nouveau, dans la double somme de (5), on peut avoir une seule dérivée partielle de x qui soit égale à 1, lorsque l’on a (6), donc en remplaçant dans (5):
\[\frac{\partial y_{ij}}{\partial x_{mn}} = w_{m-i+1,n-j+1}\]où $w$ représente notre filtre initial étendu avec des 0, lorsque l’on sort de son intervalle de définition.
En injectant cette formule dans (4) on obtient:
\[dx_{mn} = \sum_{i=1}^3 \sum_{j=1}^3 dy_{ij} \cdot w_{m-i+1,n-j+1} \tag{7}\]On va visualiser ce que cela nous donne sur quelques valeurs choisies pour les indices. Par exemple
\[\begin{align*} dx_{11} &= \sum_{i=1}^3 \sum_{j=1}^3 dy_{ij} \cdot w_{2-i,2-j}\\ &= \sum_{i=1}^3 dy_{i1} w_{2-i,1} + dy_{i2} w_{2-i,0} + dy_{i3} w_{2-i,-1,}\\ &= dy_{11} w_{1,1} + dy_{12} w_{1,0} + dy_{13} w_{1,-1}\\ &+ dy_{21} w_{0,1} + dy_{22} w_{0,0} + dy_{23} w_{0,-1}\\ &+ dy_{31} w_{-1,1} + dy_{32} w_{-1,0} + dy_{33} w_{-1,-1} \end{align*}\]En utilisant $*$ pour notation du produit de convolution, on a:
\[dx_{11} = dy * \begin{bmatrix} w_{1,1} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\]Comme les valeurs de $dy$ ne changent pas on va se limiter aux valeurs des indices de w. Pour $dx_{22}$ : $3-i,3-j$
\[\begin{bmatrix} 2,2 & 2,1 & 2,0 \\ 1,2 & 1,1 & 1,0 \\ 0,2 & 0,1 & 0,0 \end{bmatrix}\]Donc on a un produit de convolution entre dy et une matrice w’ de type:
\[\begin{bmatrix} w_{2,2} & w_{2,1} & 0 \\ w_{1,2} & w_{1,1} & 0 \\ 0 & 0 & 0 \end{bmatrix}\]Autre exemple pour essayer de clarifier les choses: $dx_{43}$, de nouveau on se limite aux valeurs des indices: $4-i,3-j$
\[\begin{bmatrix} 3,2 & 3,1 & 3,0 \\ 2,2 & 2,1 & 2,0 \\ 1,2 & 1,1 & 1,0 \\ \end{bmatrix}\] \[\begin{bmatrix} 0 & 0 & 0 \\ w_{2,2} & w_{2,1} & 0 \\ w_{1,2} & w_{1,1} & 0 \end{bmatrix}\]Et du coup pour finir $dx_{44}$
\[\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & w_{2,2} \end{bmatrix}\]Donc on voit bien apparaître un filtre w inversé. On obtient cette fois ci un produit convolutif entre $dy$ avec une bordure de 0 et $w’$, notre $w$ inversé, qui se déplace sur cette matrice avec un pas (stride) de 1.
\[w'_{ij}=w_{3-i,3-j}\] \[dx = \begin{bmatrix} 0 &0 &0 &0 &0 \\ 0 &dy_{11} &dy_{12} &dy_{13} &0\\ 0 &dy_{21} &dy_{22} &dy_{23} &0\\ 0 &dy_{31} &dy_{32} &dy_{33} &0\\ 0 &0 &0 &0 &0 \end{bmatrix} * \begin{bmatrix} w_{22} & w_{21} \\ w_{12} & w_{11} \\ \end{bmatrix}\] \[dx = dy\_0 * w' \tag{8}\]Résumé des équations de rétropropagation
\[db = \sum_{i=1}^3 \sum_{j=1}^3 dy_{ij}\] \[dw = \begin{bmatrix} x_{11} &x_{12} &x_{13} &x_{14}\\ x_{21} &x_{22} &x_{23} &x_{24} \\ x_{31} &x_{32} &x_{33} &x_{34}\\ x_{41} &x_{42} &x_{43} &x_{44} \end{bmatrix} * \begin{bmatrix} dy_{11} &dy_{12} &dy_{13} \\ dy_{21} &dy_{22} &dy_{23} \\ dy_{31} &dy_{32} &dy_{33} \end{bmatrix} = x * dy\] \[dx = \begin{bmatrix} 0 &0 &0 &0 &0 \\ 0 &dy_{11} &dy_{12} &dy_{13} &0\\ 0 &dy_{21} &dy_{22} &dy_{23} &0\\ 0 &dy_{31} &dy_{32} &dy_{33} &0\\ 0 &0 &0 &0 &0 \end{bmatrix} * \begin{bmatrix} w_{22} & w_{21} \\ w_{12} & w_{11} \\ \end{bmatrix} = dy\_0 * w'\]Cas général et prise en compte des profondeurs
Les choses se complexifient encore un peu plus lorsque l’on cherche à prendre en compte la profondeur de C canaux de x et celle de F filtres de y.
Entrées
- x: données d’entrée de dimensions (C, H, W)
- w: poids de filtres de dimensions (F, C, HH, WW)
- b: Biais de dimensions (F,)
Sortie:
- y: Données de sortie de dimension (F, H’, W’)
Les équations mathématiques multiplient les indices et en deviennent difficilement lisibles. Par exemple la propagation dans ce cas de figure donne:
\[y_{fij} = \sum_{k} \sum_{l} w_{fckl} \cdot x_{c,i+k-1,j+l-1} +b_f \tag {9}\]db
Le calcul de db reste simple et chaque $b_f$ correspond à une carte d’activation $y_f$:
\[db_f = dy_{fij}\cdot\frac{\partial y_{fij}}{\partial b_f}\] \[db_f = \sum_{i} \sum_{j} dy_{fij}\]dw
\[dw_{fckl} = dy_{fij}\cdot\frac{\partial y_{fij}}{\partial w_{fckl}}\]En injectant (9), comme la double somme n’est pas faite sur les indices de dy, on peut écrire:
\[\frac{\partial y_{fij}}{\partial w_{fckl}} = x_{c,i+k-1,j+l-1}\] \[dw_{fckl} = dy_{fij}\cdot x_{c,i+k-1,j+l-1}\]Algorithme
Pour la programmation, plutôt que de détailler l’ensemble des équations, ce qui peut certainement se faire avec un peu (beaucoup) de rigueur, on va se limiter aux intuitions que l’on a percées grâce aux exemples précédents. Et essayer de généraliser en jouant sur les dimensions. On peut comparer nos résultats avec un calcul numérique des gradients, ce qui permettra de valider la solution.
Cette solution se limite au cas où l’on a un stride = 1
Comparaison avec le calcul numérique du gradient
Testing conv_backward_naive function
dx error: 7.489787768926947e-09
dw error: 1.381022780971562e-10
db error: 1.1299800330640326e-10
Erreur proche de 0 à chaque fois, ce qui valide notre algorithme ! :)
Généralisation pour tout stride - Nouvel article?
Dans cette version on regarde la contribution de chaque volume d’entrée au résultat y et on rétropropage en calculant des produits de convolution entre volumes de tailles identiques. Dans ce cas on a dx_input_volume = dy[i,j] . w (. est ici un simple produit). On cumule ensuite toutes les contributions dx qui participent aux mêmes indices. Finalement c’est beaucoup plus simple dans la mise en oeuvre que la version mathématique appliquée sur l’ensemble des valeurs de x.
Voici une version sans vectorisation, particulièrement lente, mais cela permet de voir comment les choses se mettent en place. Que ce soit pour dw ou dx, on se limite pour le coeur du calcul à l’influence du produit de convolution de deux éléments de taille identique (qui donnent un scalaire), et on cumule ensuite lors des déplacements du filtre sur l’entrée x pendant la propagation.
pour x et w de mêmes dimensions, y est un scalaire: